DAY 23 試題

問題描述

在一個 m x n 的矩形島嶼上，這個島嶼的左邊和上邊邊界接壤太平洋，而右邊和下邊邊界接壤大西洋。島嶼被劃分為一個由正方形單元格組成的網格，給定一個 m x n 的整數矩陣 heights，其中 heights[r][c] 表示座標 (r, c) 上單元格的海拔高度。

島嶼經常下雨，雨水可以從當前單元格流向相鄰的北、南、東或西單元格，前提是相鄰單元格的高度小於等於當前單元格的高度。雨水可以從任何相鄰海洋的單元格流入海洋。

請返回一個 2D 清單 result，其中 result[i] = [ri, ci] 表示雨水可以從單元格 (ri, ci) 流向太平洋和大西洋。

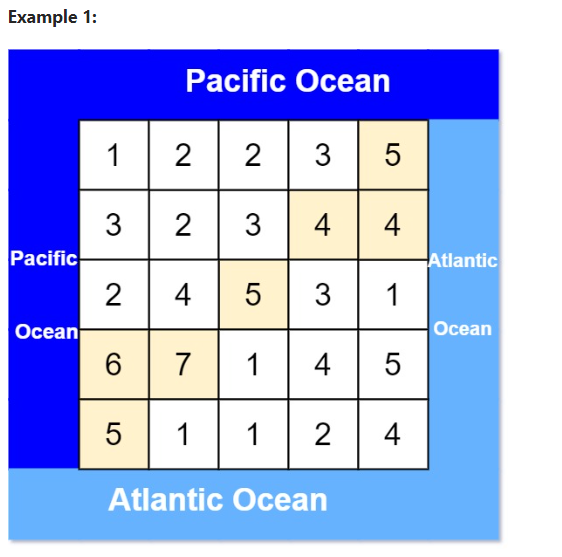
範例 1：

• 輸入：heights = [[1,2,2,3,5],[3,2,3,4,4],[2,4,5,3,1],[6,7,1,4,5],[5,1,1,2,4]]
• 輸出：[[0,4],[1,3],[1,4],[2,2],[3,0],[3,1],[4,0]]
• 解釋：
  • [0,4] : 水流可同時到達太平洋和大西洋。
  • [1,3] : 水流從 [1,3] 經過 [0,3] 到達太平洋，同時經過 [1,4] 到達大西洋。

範例 2：

• 輸入：heights = [[1]]
• 輸出：[[0,0]]
• 解釋：水流可以從唯一的單元格同時流向太平洋和大西洋。

解題思路

這個問題的核心在於找出哪些座標的水可以同時流向太平洋和大西洋。具體來說，我們可以分別從太平洋和大西洋的邊界進行反向搜索，並記錄哪些座標的水能夠到達兩個海洋。最終，兩個集合的交集即為結果。
詳細步驟：

1. 反向搜索：

• 從接壤太平洋的邊界（左邊和上邊）開始，使用 DFS 或 BFS 標記所有可以流向太平洋的座標。
• 同理，從接壤大西洋的邊界（右邊和下邊）開始，標記所有可以流向大西洋的座標。

2. 判斷交集：

• 將能夠流向太平洋和大西洋的座標求交集，這些座標就是結果。

3. 鄰居檢查：

• 當我們從某個座標開始搜索時，會向四個方向檢查相鄰的單元格，只有當相鄰單元格的高度小於等於當前單元格時，才能繼續搜索。

class Solution {
public:
    vector<vector<int>> pacificAtlantic(vector<vector<int>>& heights) {
        int m = heights.size();
        int n = heights[0].size();
        vector<vector<bool>> pacific(m, vector<bool>(n, false));
        vector<vector<bool>> atlantic(m, vector<bool>(n, false));
        vector<vector<int>> result;
        
        // 定義方向：上、下、左、右
        vector<int> directions = {-1, 0, 1, 0, -1};
        
        // 深度優先搜索 (DFS) 函數
        function<void(int, int, vector<vector<bool>>&)> dfs = [&](int r, int c, vector<vector<bool>>& ocean) {
            ocean[r][c] = true;
            for (int i = 0; i < 4; i++) {
                int nr = r + directions[i];
                int nc = c + directions[i+1];
                if (nr >= 0 && nr < m && nc >= 0 && nc < n && !ocean[nr][nc] && heights[nr][nc] >= heights[r][c]) {
                    dfs(nr, nc, ocean);
                }
            }
        };
        
        // 從太平洋邊界開始搜索
        for (int i = 0; i < m; i++) {
            dfs(i, 0, pacific);  // 左邊
            dfs(i, n - 1, atlantic);  // 右邊
        }
        for (int j = 0; j < n; j++) {
            dfs(0, j, pacific);  // 上邊
            dfs(m - 1, j, atlantic);  // 下邊
        }
        
        // 將可以流向兩個海洋的座標加入結果
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (pacific[i][j] && atlantic[i][j]) {
                    result.push_back({i, j});
                }
            }
        }
        
        return result;
    }
};

解法重點與分析

1. 深度優先搜索 (DFS)：透過從海洋的邊界開始，利用 DFS 搜索能夠流向每個海洋的座標，這樣可以反向追溯水的流動過程。
2. 反向思維：問題中描述的是水如何從內部流向兩個海洋，但我們實際上是從兩個海洋的邊界反向追蹤，這樣可以更有效地解決問題。
3. 時間複雜度：O(m * n)，每個單元格最多被訪問兩次，一次是從太平洋邊界，一次是從大西洋邊界。
4. 空間複雜度：O(m * n)，用來存儲兩個標記矩陣（太平洋和大西洋）。

總結

此題主要考察如何有效處理多方向的流動問題。透過 DFS 和反向思維，我們可以將原本的問題轉化為從海洋邊界開始搜索的問題，從而高效地找到解答。最終，我們根據標記矩陣來確定哪些座標可以同時流向太平洋和大西洋。

以上是第二十三天的自學內容分享，謝謝大家。